本文共 2547 字,大约阅读时间需要 8 分钟。
疯狂创客圈 Java 高并发【 亿级流量聊天室实战】实战系列 【 】
架构师成长+面试必备之 高并发基础书籍 【 】
Crazy-SpringCloud 微服务脚视频&环境搭建介绍:
疯狂创客圈 Crazy-SpringCloud 微服务脚手架,是为 Java 微服务开发 入门者 准备的 学习和开发脚手架。并配有一系列的使用教程和视频,大致如下:
高并发 环境搭建 图文教程和演示视频,陆续上线:
| 中间件 | 链接地址 |
|---|---|
| Linux Redis 安装(带视频) | |
| Linux Zookeeper 安装(带视频) | |
| Windows Redis 安装(带视频) | |
| RabbitMQ 离线安装(带视频) | |
| ElasticSearch 安装, 带视频 | |
| Nacos 安装(带视频) |
Crazy-SpringCloud 微服务脚手架 图文教程和演示视频,陆续上线:
| 组件 | 链接地址 |
|---|---|
| Eureka | |
| SpringCloud Config | |
| spring security | |
| Spring Session | |
| 分布式 session 基础 | |
| 重点: springcloud 开发脚手架 | |
| SpingSecurity + SpringSession 死磕 (写作中) |
小视频以及所需工具的百度网盘链接,请参见
前言:SpringCloud 热部署 热加载 热调试
有两种方式:
一: devtools的热部署
【这是一种假的热部署,说白了就是重启一下】
二. jrebel 的热部署
很牛逼,但是需要破解哦
方式一:devtools 的热部署
每修改一下代码再去 run一次, 实在是很麻烦. 很浪费时间. 很低效
但既然用这个框架的,它所包含的特性什么的还是要充分利用,不能浪费呀!
springboot的热部署网上有太多的教案,在此呢,也只是真实记录一下自己在实际操作过程中的方法步骤。
1、pom.xml配置,这是一定要配置的
热加载在pom.xml中添加devtools的maven引用,同时在plugin中添加devtools生效标志
org.springframework.boot spring-boot-devtools org.springframework.boot spring-boot-maven-plugin true build-info
2、Idea设置
于热部署是监听 Class 文件的变化,它自身不会主动去编译 Java 文件,所以我们得在 Java 文件改动时,自动编译成 Class 文件,然后热部署工具创造的新的类加载器才会加载改变后的 Class 文件。
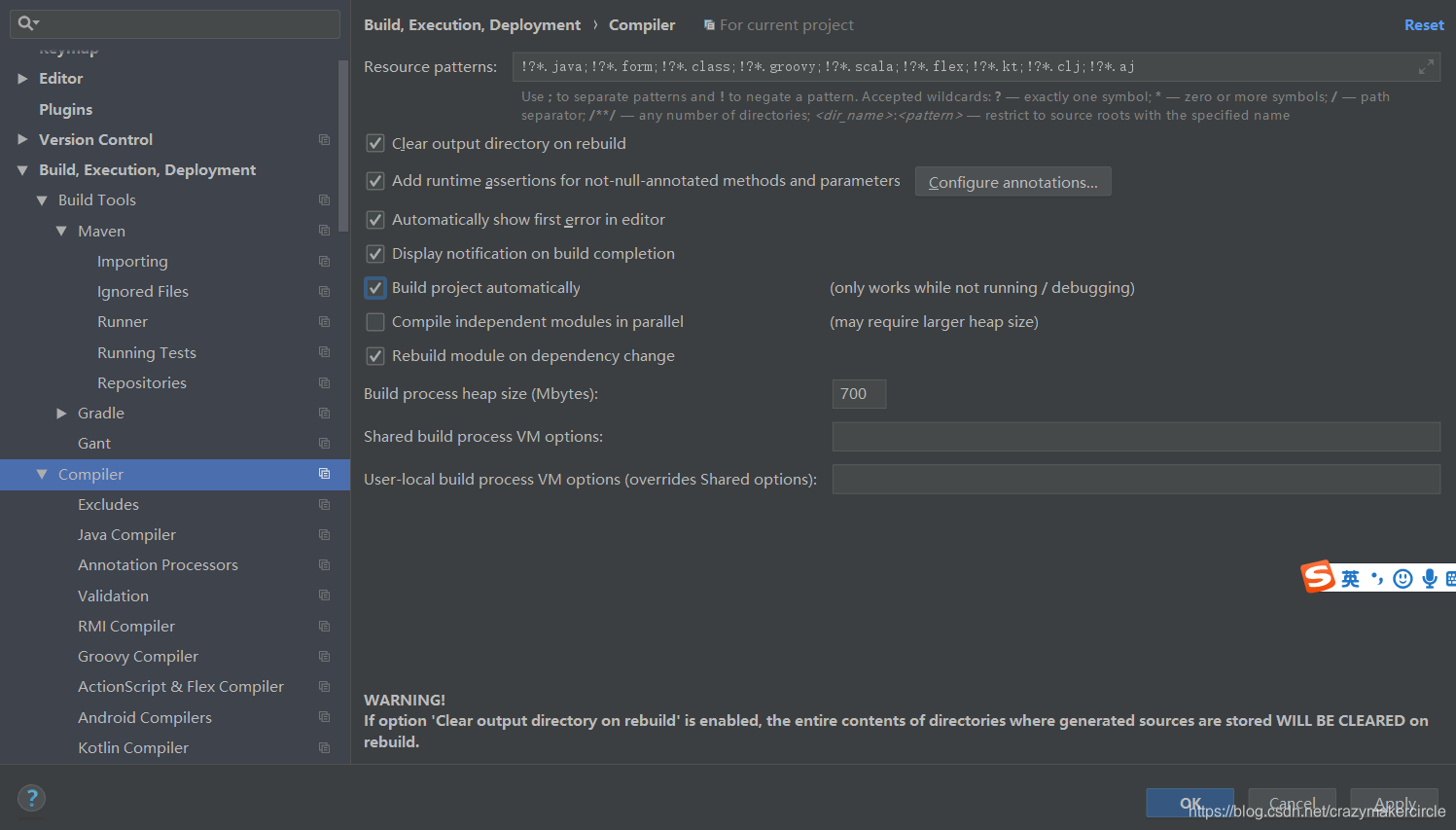
所以,如果你使用 IDEA 开发工具的话,记得要把自动编译打开。
File | Settings | Build, Execution, Deployment | Compiler :该√的√上
3、修改IDEA的 Registry
开启自动编译,还差一步。
所以,如果你使用 IDEA 开发工具的话,记得要把自动编译打开。
再执行 shift+ctrl+alt+/ 快捷键

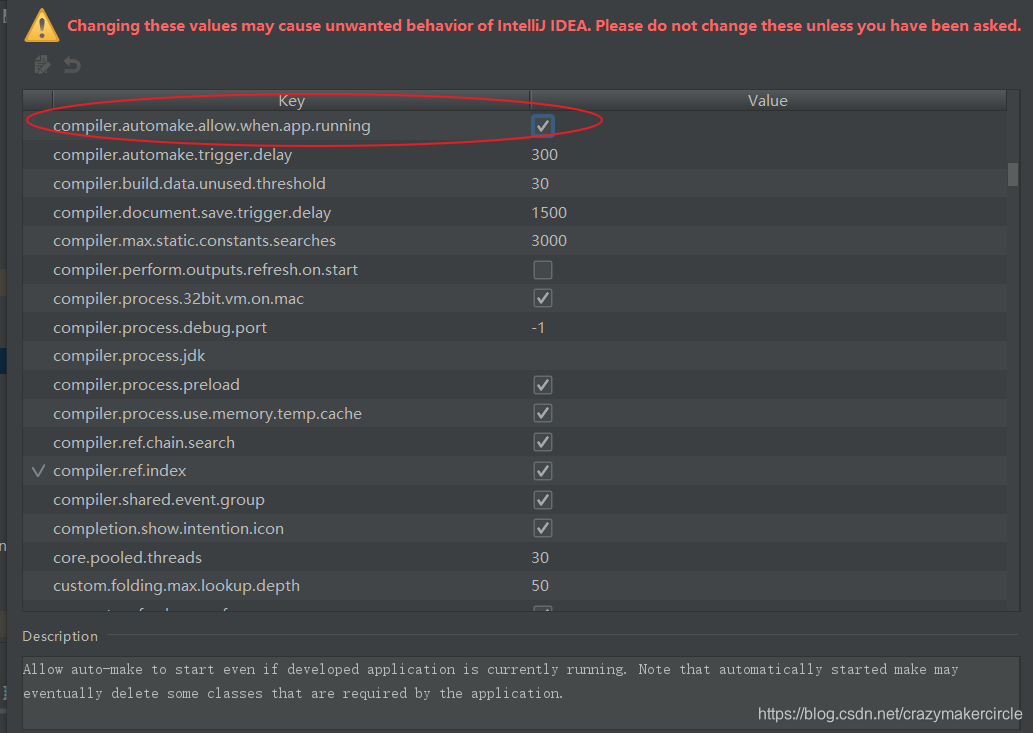
在配置文件application.yml
热部署生效:在配置文件application.yml中添加 :
spring: devtools: restart: enabled: true #设置开启热部署
4 重启idea,运行工程
注意:这种配置启动不能直接运行 main 方法了,需要使用 mvn spring-boot:run 启动,
运行:mvn clean spring-boot:run
问题:
springBoot框架 只是实现了热启动而已,从控制台日志就可以看出来。
方式二: JRebel插件热部署
可以在csdn下载离线插件:
也可以使用idea安装在线插件:
开发工具idea中使用JRebel插件
JRebel是JavaEE中比较流行的热部署插件,可快速实现热部署,节省了大量重启时间,提高了个人开发效率。
1、点击File -> Settings -> Plugins,如下图:搜索JRebel安装
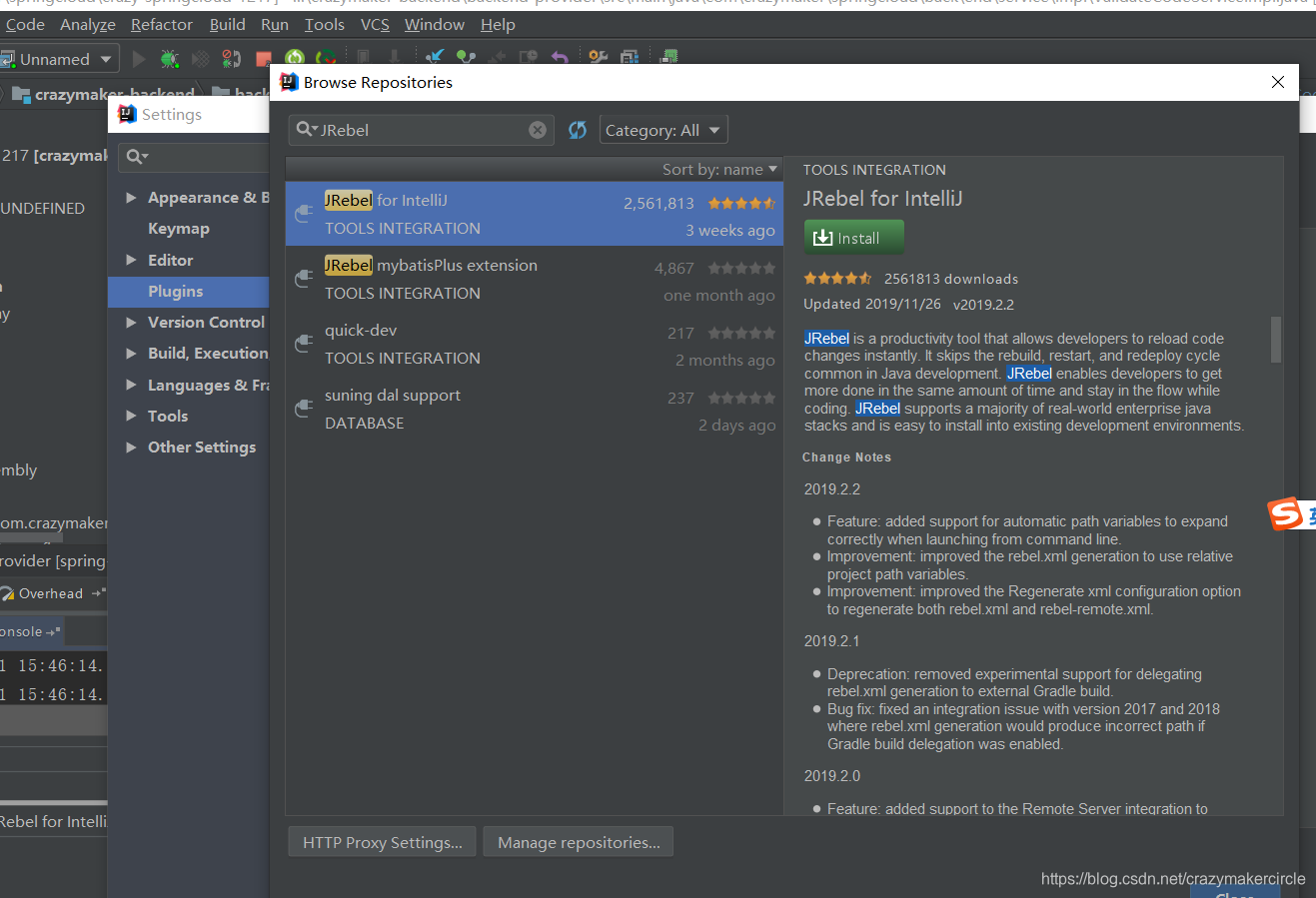
jrebel 的激活和使用
1、重启idea,右上角即出现快捷按钮,分别是run、debug模式
2 第一次使用是,需要 激活
jrebel 的激活地址,请参见博客
激活需要生成GUID, 生成一个GUID
在线生成GUID地址, , PS:如果失效刷新GUID替换就可以!
3 激活之后,也可以右键springboot的启动类:
又或者使用spring的运行面板:
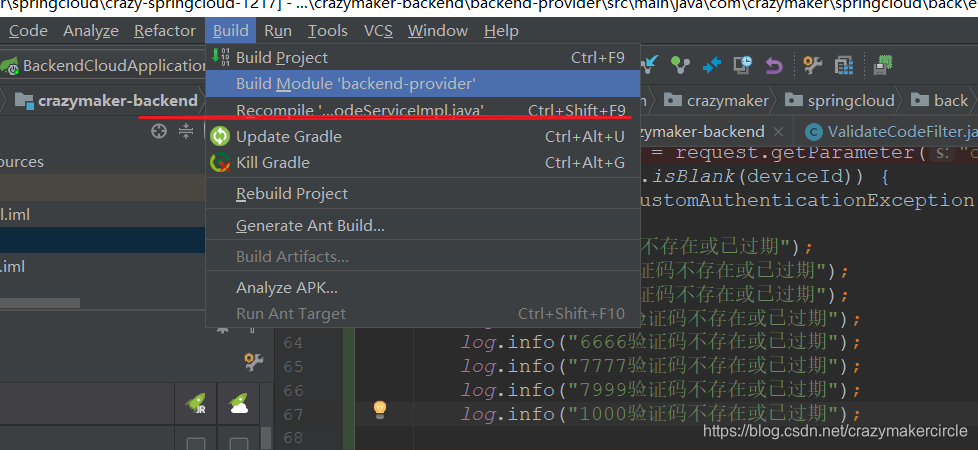
手动编译要加载的类
如果配置了自动编译,这一步,直接忽略
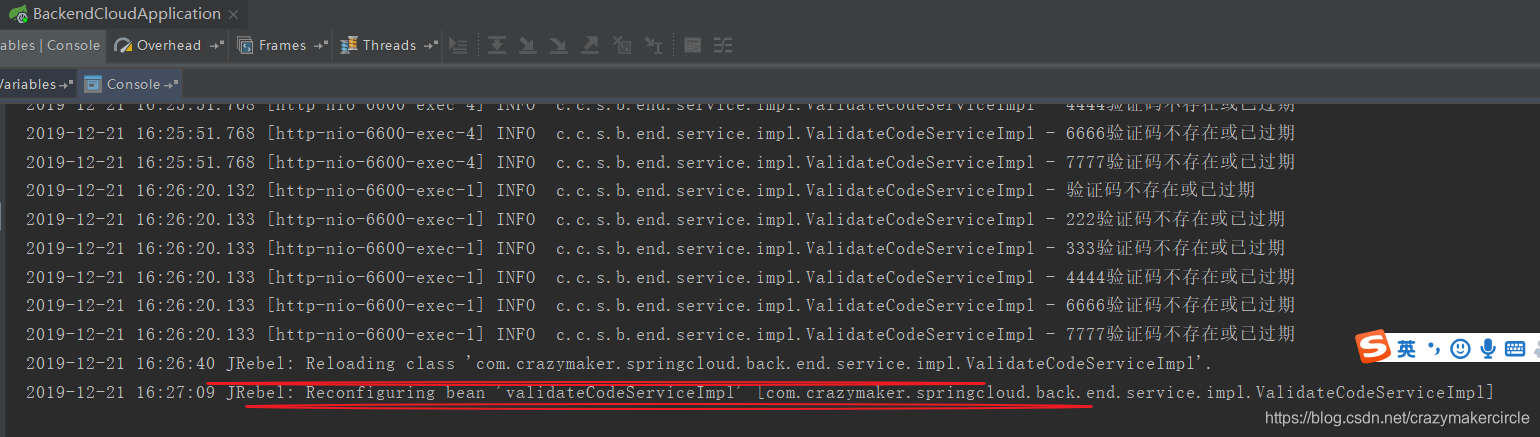
jrebel自动加载class,自动配置bean
代码重新编译后,jrebel自动加载class,自动配置bean
设置为离线模式
然后将JRebel设置为离线模式,可以180天内不用再次激活,如下图
高并发IM,高并发秒杀,请关注 Java 高并发研习社群 【 】
最后,介绍一下疯狂创客圈:疯狂创客圈,一个Java 高并发研习社群 【 】
疯狂创客圈,倾力推出:面试必备 + 面试必备 + 面试必备 的基础原理+实战 书籍 《》
疯狂创客圈 Java 死磕系列
- Java (Netty) 聊天程序【 亿级流量】实战 开源项目实战
-
Netty 源码、原理、JAVA NIO 原理
-
Java 面试题 一网打尽
-
疯狂创客圈
QyNy05NTY0MjQxMjQuanBn?x-oss-process=image/format,png)
疯狂创客圈 Java 死磕系列
- Java (Netty) 聊天程序【 亿级流量】实战 开源项目实战
-
Netty 源码、原理、JAVA NIO 原理
-
Java 面试题 一网打尽
-
疯狂创客圈